Medidas de Dispersão: Amplitude, Variância e Desvio Padrão. Entenda a Variabilidade dos Seus Dados.

0.0 Introdução: Por Que a Média Sozinha Não Conta a História Completa?

Em epidemiologia e saúde pública, a capacidade de tomar decisões informadas depende diretamente da nossa habilidade de interpretar dados corretamente [3, 5]. Frequentemente, recorremos a medidas de tendência central, como a média, para resumir um conjunto de informações. No entanto, confiar apenas na média é como descrever o clima de uma cidade utilizando somente sua temperatura média anual; ignoramos as ondas de calor escaldantes e as noites de frio congelante que definem a experiência real de viver lá. Uma medida de tendência central, sem uma medida de dispersão que a acompanhe, oferece uma visão incompleta e potencialmente enganosa da realidade. As medidas de dispersão são as ferramentas estatísticas que quantificam a variabilidade, o “espalhamento” ou a “heterogeneidade” dos dados, revelando se os valores estão firmemente agrupados em torno da média ou amplamente dispersos. Em essência, elas nos informam sobre a confiabilidade e a precisão de uma medida central, completando o panorama estatístico. Para iniciar nossa análise, exploraremos as medidas de dispersão mais simples e intuitivas.

1.0 Medidas Simples de Dispersão: Um Ponto de Partida

Antes de mergulharmos nas medidas estatisticamente mais robustas e informativas, é fundamental compreender as formas mais diretas de quantificar a dispersão. A Amplitude e o Intervalo Interquartil (IIQ) representam os primeiros passos nessa jornada, oferecendo uma avaliação rápida e intuitiva da variabilidade de um conjunto de dados. Elas nos fornecem uma base conceitual sólida para entender por que, em muitas situações, precisamos de ferramentas mais sofisticadas. Embora úteis para uma análise preliminar, essas medidas simples possuem limitações importantes que motivam o uso de instrumentos mais poderosos, como o desvio padrão, para uma análise mais completa e precisa.

1.1 Amplitude (Range): A Visão Mais Rápida, Porém Limitada

A Amplitude é definida como a diferença entre o maior e o menor valor em um conjunto de dados. Sua principal vantagem reside na simplicidade e na rapidez de seu cálculo, oferecendo um panorama instantâneo da extensão total coberta pelos dados. Por exemplo, se a idade dos pacientes em um grupo varia de 22 a 85 anos, a amplitude é de 63 anos.

Contudo, sua principal desvantagem é a extrema sensibilidade a valores atípicos (outliers). Um único valor extremo pode distorcer drasticamente a percepção da variabilidade geral. Imagine um grupo de cinco pacientes com as seguintes idades: 25, 28, 30, 32 e 85 anos. A amplitude aqui é de 60 anos (85 – 25), sugerindo uma enorme dispersão. No entanto, se removermos o paciente de 85 anos, a amplitude dos quatro restantes seria de apenas 7 anos (32 – 25), revelando um grupo muito mais homogêneo. Essa vulnerabilidade torna a amplitude uma medida pouco robusta e raramente utilizada como a principal métrica de dispersão na maioria das análises de saúde.

1.2 O Intervalo Interquartil (IIQ): Focando no Coração dos Dados

Para superar a limitação da amplitude, utilizamos os quartis. Quartis são pontos que dividem um conjunto de dados ordenado em quatro partes iguais.

• Primeiro Quartil (Q1): O valor que deixa 25% dos dados abaixo dele.
• Segundo Quartil (Q2): A mediana, que divide os dados ao meio (50% abaixo).
• Terceiro Quartil (Q3): O valor que deixa 75% dos dados abaixo dele.

O Intervalo Interquartil (IIQ) é então definido como a diferença entre o terceiro e o primeiro quartil: IIQ = Q3 - Q1.

O grande valor do IIQ como medida de dispersão é que ele representa a amplitude dos 50% centrais dos dados. Ao ignorar os 25% de valores mais baixos e os 25% de valores mais altos, o IIQ é completamente imune a outliers. Ele foca no “coração” da distribuição, onde a maioria dos dados se concentra, oferecendo uma medida de variabilidade muito mais estável e confiável do que a amplitude total, visualizada de forma clara pela ‘caixa’ em um diagrama de boxplot.

——————————————————————————–

Mínimo --- [ Q1 | Mediana (Q2) | Q3 ] --- Máximo
              <----   IIQ   ---->

——————————————————————————–

Essa robustez torna o Intervalo Interquartil o parceiro ideal para a Mediana na descrição de dados que possuem distribuições assimétricas, onde a presença de valores extremos tornaria a média e a amplitude total medidas enganosas.

2.0 O Ouro da Dispersão: Variância e Desvio Padrão

——————————————————————————–

Entramos agora no território das medidas de dispersão mais importantes e amplamente utilizadas na estatística: a Variância e o Desvio Padrão. Elas são a base para inúmeros testes de hipóteses e modelos estatísticos, especialmente quando lidamos com dados que seguem uma distribuição simétrica (ou “normal”). Diferentemente da amplitude e do IIQ, a variância e o desvio padrão levam em consideração todos os pontos de dados em seu cálculo, fornecendo uma medida de dispersão muito mais completa. Entender a lógica por trás de seu cálculo é essencial para interpretar corretamente a vasta maioria da literatura científica no campo da saúde.

2.1 A Lógica da Variância: Quantificando o Desvio Total

Conceitualmente, a variância representa a média dos quadrados dos desvios de cada ponto de dado em relação à média do conjunto ((x - x̄)²) [1]. A lógica de elevar cada desvio ao quadrado é dupla e engenhosa:

1. Elimina os Sinais Negativos: Garante que todos os desvios se tornem positivos. Sem isso, os desvios de valores abaixo da média (negativos) poderiam anular os desvios de valores acima da média (positivos), resultando em uma soma próxima de zero e mascarando a verdadeira variabilidade.
2. Penaliza Desvios Maiores: Ao elevar ao quadrado, os valores que estão muito distantes da média contribuem muito mais para a variância total do que os valores próximos. Isso dá um peso maior aos pontos de dados mais extremos.

Apesar de sua importância matemática, a variância possui uma limitação prática significativa: sua unidade de medida é o quadrado da unidade original dos dados. Se estivermos medindo o peso dos pacientes em quilogramas (kg), a variância será expressa em kg², uma unidade que não possui interpretação intuitiva no mundo real.

2.2 Desvio Padrão (DP): A Medida Padrão de Variabilidade

O Desvio Padrão (DP), representado por s ou a letra grega sigma (σ), é a solução direta para o problema de interpretação da variância. Ele é definido simplesmente como a raiz quadrada da variância.

Ao extrair a raiz quadrada, o Desvio Padrão retorna à unidade de medida original dos dados (de kg² de volta para kg). Isso o torna a medida de dispersão mais poderosa e popular, pois é diretamente interpretável e comparável com a média. Em suma, a interpretação do desvio padrão é a seguinte: ele representa, em média, o quão distante cada observação no conjunto de dados está da média geral.

• Um DP baixo indica que os dados estão firmemente agrupados perto da média, sugerindo consistência e baixa variabilidade.
• Um DP alto indica que os dados estão espalhados por uma ampla gama de valores, sugerindo alta variabilidade e heterogeneidade.

2.3 A Regra Empírica (68-95-99.7): Decodificando o Desvio Padrão

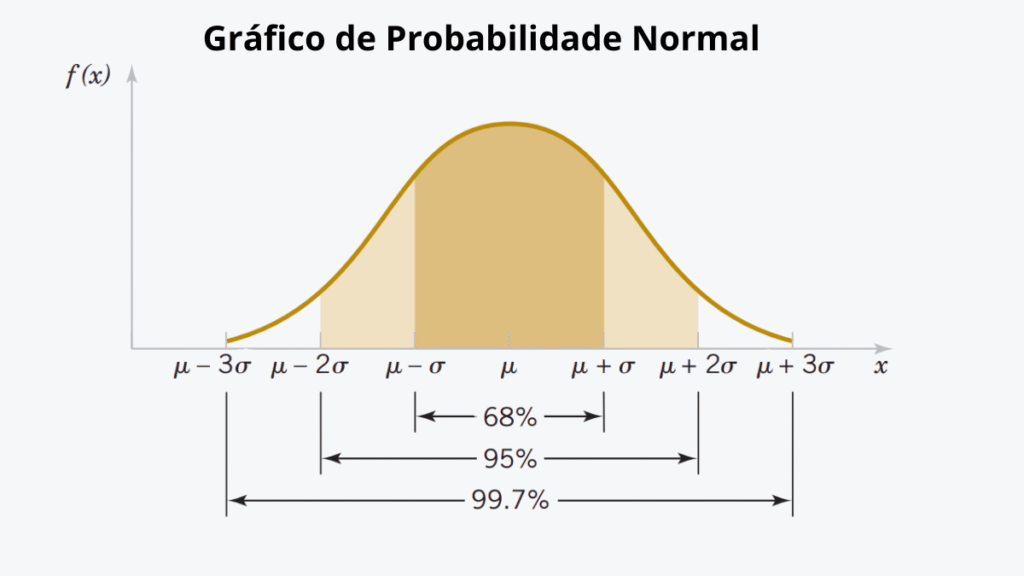
Para dados que seguem uma distribuição aproximadamente normal (com o clássico formato de sino), o desvio padrão ganha um poder interpretativo ainda maior graças à Regra Empírica. Esta regra nos permite visualizar rapidamente como os dados estão distribuídos em torno da média [1]:

• Aproximadamente 68% dos dados estão a 1 desvio padrão da média (no intervalo entre média - 1 DP e média + 1 DP).
• Aproximadamente 95% dos dados estão a 2 desvios padrão da média (no intervalo entre média - 2 DP e média + 2 DP). Por exemplo, para um teste de QI com média 100 e DP 15, aproximadamente 95,44% dos valores estariam entre 70 e 130 (média ± 2 DP) [1].
• Aproximadamente 99.7% dos dados estão a 3 desvios padrão da média (no intervalo entre média - 3 DP e média + 3 DP).

Essa regra é uma ferramenta poderosa. Ela permite que, apenas com a média e o desvio padrão, possamos mentalmente “desenhar” a distribuição dos dados, estimar a proporção de valores em diferentes faixas e identificar observações que são estatisticamente incomuns (aquelas que caem fora de ±2 ou ±3 DP da média).

3.0 A Combinação Vencedora: Dispersão e Centralidade Juntas

A lição mais importante da análise descritiva é que a escolha da medida de tendência central e da medida de dispersão não é arbitrária. Ela é ditada pela forma da distribuição dos dados. Relatar a combinação correta de medidas é um pilar da boa prática científica, garantindo que os resultados sejam comunicados honesta e precisamente. A seguir, detalhamos os dois cenários principais que você encontrará na prática, fornecendo um guia sobre como relatar seus achados de maneira profissional. Compreender essa escolha é fundamental para evitar interpretações equivocadas e conduzir análises rigorosas.

3.1 O Critério da Distribuição: Um Guia Prático

Cenário 1: Distribuições Simétricas (ou Normais)

• Para dados que se assemelham a um formato de “sino”, a Média é a medida de tendência central mais apropriada, pois representa o ponto de equilíbrio da distribuição.
• Seu parceiro inseparável é o Desvio Padrão (DP), que quantifica perfeitamente a dispersão em torno dessa média.
• Instrução de Relato: Sempre apresente os resultados como Média (± DP). Exemplo: “A idade média dos participantes foi de 45.2 (± 10.1) anos.”

Cenário 2: Distribuições Assimétricas

• Quando os dados são assimétricos (com uma “cauda” longa para um lado), a média é fortemente influenciada por valores extremos e deixa de ser um bom representante do centro dos dados.
• Nesses casos, a Mediana é a medida de tendência central mais robusta e representativa, pois indica o ponto exato que divide os dados em duas metades iguais, independentemente dos valores extremos.
• A medida de dispersão correta é o Intervalo Interquartil (IIQ), que descreve a variabilidade dos 50% centrais dos dados, sendo também robusto a outliers.
• Instrução de Relato: Sempre apresente os resultados como Mediana (IIQ). Exemplo: “O tempo de internação hospitalar foi de 8 (IIQ: 5-15) dias.”

3.2 Tabela Resumo: Guia de Relato (Como Publicar Corretamente)

Para facilitar a consulta, a tabela a seguir resume a combinação ideal de medidas a serem relatadas com base na distribuição dos dados.

Tipo de Distribuição dos Dados	Medida de Tendência Central	Medida de Dispersão Apropriada
Simétrica (Normal)	Média	Desvio Padrão (DP)
Assimétrica	Mediana	Intervalo Interquartil (IIQ)

4.0 Exemplo Aplicado em Epidemiologia: Análise de Variabilidade Glicêmica

A aplicação de conceitos estatísticos em cenários clínicos reais revela seu verdadeiro poder. Muitas vezes, a dispersão dos dados possui implicações de saúde tão ou mais importantes que o valor médio. Vamos analisar um cenário hipotético, mas clinicamente plausível, para ilustrar este ponto.

Imagine um ensaio clínico que compara a eficácia de dois novos medicamentos (Medicamento A e Medicamento B) para diabetes tipo 2. O desfecho principal é o controle glicêmico, medido pela glicemia de jejum (em mg/dL) dos pacientes após 6 meses de tratamento. Os resultados estão resumidos na tabela abaixo:

Medicamento	Glicemia Média (mg/dL)	Desvio Padrão (DP) da Glicemia (mg/dL)
Medicamento A	120	5
Medicamento B	120	25

À primeira vista, olhando apenas para a glicemia média, os dois medicamentos parecem igualmente eficazes, atingindo um excelente controle de 120 mg/dL. No entanto, a história real e clinicamente relevante está no desvio padrão.

• Medicamento A (DP = 5 mg/dL): Um desvio padrão baixo indica um controle glicêmico estável e previsível. Os níveis de glicose dos pacientes permanecem consistentemente próximos da média segura de 120 mg/dL. Isso minimiza o risco de complicações e oferece grande segurança ao paciente e ao médico.
• Medicamento B (DP = 25 mg/dL): Um desvio padrão cinco vezes maior indica um controle glicêmico instável e errático. Embora a média seja 120 mg/dL, isso ocorre porque os pacientes experimentam grandes oscilações: muitos episódios de hiperglicemia (valores muito altos, como 170 mg/dL) são “compensados” por episódios de hipoglicemia (valores perigosamente baixos, como 60 mg/dL). A hipoglicemia severa é uma emergência médica que pode levar a convulsões, coma e até a morte.

Conclusão Clínica: Apesar de apresentar a mesma média, o Medicamento B é clinicamente inferior e significativamente mais perigoso devido à sua alta variabilidade. Este exemplo demonstra inequivocamente que a análise da dispersão não é um mero exercício acadêmico; é uma etapa essencial para a tomada de decisão segura e eficaz em saúde.

5.0 Conclusão: A Dispersão Como Medida de Certeza

Ao longo deste material, estabelecemos que descrever a variabilidade dos dados é tão fundamental quanto descrever sua tendência central. A dispersão, em sua essência, funciona como uma medida de incerteza. Um desvio padrão elevado não indica apenas que os dados estão espalhados; ele sinaliza uma menor previsibilidade e consistência nos resultados. Essa ideia se conecta diretamente a um dos conceitos mais importantes da inferência estatística: o Intervalo de Confiança [2].

Uma alta dispersão nos dados da amostra (alto DP) leva a um erro padrão da média maior, que, por sua vez, resulta em um Intervalo de Confiança de 95% (IC 95%) mais largo. Essa conexão é direta, pois o erro padrão da média é calculado dividindo-se o desvio padrão pela raiz quadrada do tamanho da amostra (EP = DP/√n). Portanto, um DP mais alto resulta inevitavelmente em um erro padrão maior, ampliando o intervalo em que a verdadeira média da população provavelmente se encontra. Em termos práticos, um IC 95% largo significa que temos menor precisão em nossa estimativa da verdadeira média populacional. A nossa “certeza” sobre o resultado diminui, o poder estatístico do estudo é reduzido e a confiança em nossas conclusões fica comprometida. Portanto, ao analisar e relatar sempre as medidas de dispersão apropriadas, não estamos apenas descrevendo dados; estamos qualificando a certeza de nossas descobertas e praticando uma ciência mais rigorosa, transparente e clinicamente relevante [4].

6.0 Referências Bibliográficas

1. Vieira S. Introdução à Bioestatística. 5ª ed. Rio de Janeiro: GEN | Guanabara Koogan; 2018.
2. Vu T, Harrington D. Biostatistics for Clinical and Public Health Research. Boca Raton: Chapman and Hall/CRC; 2021.
3. Almeida-Filho N, Barreto ML, organizadores. Epidemiologia & Saúde: Fundamentos, Métodos e Aplicações. Rio de Janeiro: Guanabara Koogan; 2012.
4. Paim JS, Almeida-Filho N. Saúde Coletiva: Teoria e Prática. Rio de Janeiro: MedBook; 2014.
5. Medronho RA, organizador. Epidemiologia. 2ª ed. São Paulo: Atheneu; 2009.