Distribuição de Dados em Epidemiologia: Guia Completo para Análise Estatística

Tabela de Conteúdo

• Introdução: Decifrando a Linguagem dos Dados em Saúde Coletiva
• 1. Por Que a Distribuição de Dados é o Ponto de Partida na Epidemiologia?
• 2. A Pedra Angular da Bioestatística: A Distribuição Normal
• 3. O Mundo Binário: Entendendo a Distribuição Binomial
• 4. Contando Eventos Raros: A Distribuição de Poisson
• Conclusão: A Distribuição de Dados Como Bússola Analítica
• FAQ: Perguntas e Respostas sobre Distribuição de Dados

——————————————————————————–

Introdução: Decifrando a Linguagem dos Dados em Saúde Coletiva

Antes de aplicar qualquer teste estatístico complexo ou construir modelos preditivos sofisticados, o primeiro passo fundamental para todo epidemiologista é compreender a forma e a estrutura dos seus dados. Este passo inicial, muitas vezes subestimado, é o que garante a robustez e a validade de toda a investigação. O conceito central nesta etapa é a distribuição de dados, que pode ser entendida como a “personalidade” dos números coletados. Ela revela padrões, tendências centrais, dispersões e anomalias, fornecendo um roteiro essencial para a interpretação correta dos fenômenos de saúde. Este guia completo irá desmistificar os principais tipos de distribuição — Normal, Binomial e Poisson — e demonstrar sua aplicação prática e indispensável no campo da saúde coletiva.

1. Por Que a Distribuição de Dados é o Ponto de Partida na Epidemiologia?

Compreender a distribuição de dados não é um mero exercício acadêmico, mas uma etapa crítica que fundamenta a escolha de métodos de análise, a validade das conclusões e a própria formulação de hipóteses em estudos epidemiológicos. A literatura especializada enfatiza a necessidade de uma “verificação preliminar da distribuição das variáveis de interesse”, pois essa análise inicial define toda a estratégia analítica subsequente. Ignorar essa etapa é como tentar navegar sem uma bússola: as chances de chegar a uma conclusão equivocada são imensas.

A importância estratégica de analisar a distribuição dos dados pode ser resumida nos seguintes pontos:

• Fundamento para a Inferência: O objetivo principal da epidemiologia é tirar conclusões sobre uma população a partir de uma amostra. A forma como os dados se distribuem na amostra oferece pistas importantes sobre a provável distribuição na população maior, garantindo que as inferências sejam representativas.
• Escolha do Teste Estatístico: A identificação da distribuição é obrigatória para decidir entre testes paramétricos (que assumem uma distribuição específica, como a normal) e não paramétricos. A consequência de uma escolha errada é grave: usar um teste paramétrico como o teste-t em uma variável não normal (por exemplo, dados assimétricos de custos de saúde) pode inflar a taxa de erro Tipo I. Isso significa que um pesquisador pode concluir falsamente que uma nova intervenção é eficaz, levando ao desperdício de recursos ou à adoção de uma política inútil. É por isso que a verificação preliminar da distribuição é um passo inegociável na análise rigorosa.
• Visualização e Compreensão: Ferramentas gráficas, como o histograma, são essenciais para visualizar a distribuição de dados. Elas permitem uma interpretação rápida e intuitiva da forma dos dados, ajudando a identificar padrões centrais, simetria, assimetria e a presença de valores atípicos (outliers) que poderiam distorcer as análises.
• Modelagem de Fenômenos: Diferentes fenômenos de saúde seguem padrões distintos. A ocorrência de um desfecho binário (doente/sadio) não se comporta da mesma forma que a medição da pressão arterial. Reconhecer que distribuições teóricas modelam diferentes tipos de eventos permite a criação de modelos estatísticos mais precisos e realistas.

Entendida sua importância fundamental, vamos explorar o tipo de distribuição mais conhecido e central para toda a estatística.

2. A Pedra Angular da Bioestatística: A Distribuição Normal

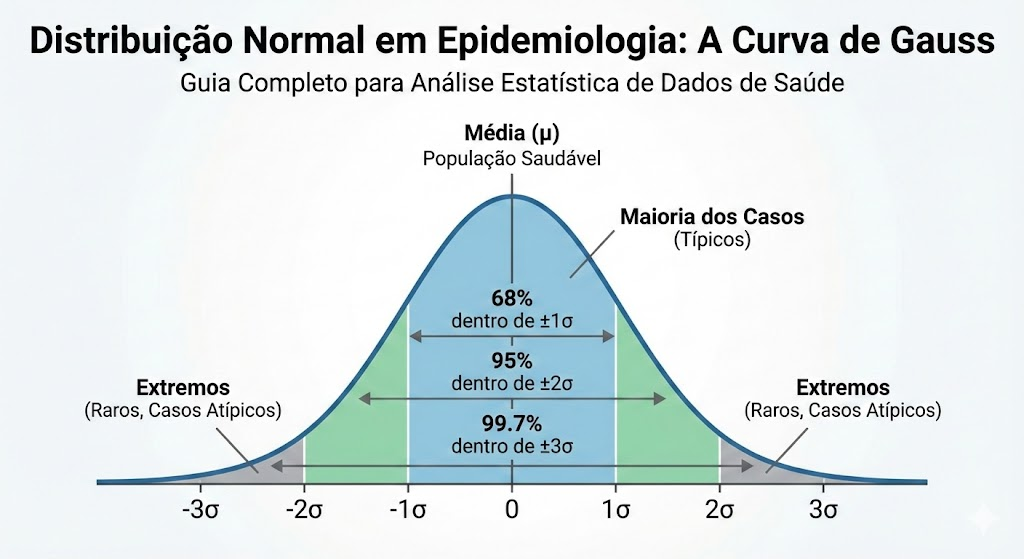
A Distribuição Normal, também conhecida como Curva de Gauss, é sem dúvida a mais icônica e fundamental em todo o campo da estatística. Sua proeminência não é arbitrária; ela deriva do poderoso Teorema do Limite Central. O poder do teorema é que ele nos permite fazer inferências sobre a média de uma variável (como a pressão arterial média em uma amostra) usando a distribuição normal, mesmo que as medições individuais de pressão arterial não sejam perfeitamente normais. Na prática, isso significa que muitos fenômenos biológicos e de saúde, quando medidos em amostras suficientemente grandes, naturalmente se aproximam dessa distribuição em forma de sino.

Características Principais

As propriedades da curva normal são bem definidas e universalmente reconhecidas, tornando-a um modelo poderoso para variáveis quantitativas contínuas.

1. Simetria: A curva é perfeitamente simétrica em torno de sua média. Isso significa que a média, a mediana e a moda dos dados são iguais e localizadas no ponto central da distribuição.
2. Parâmetros Centrais: A distribuição é completamente definida por apenas dois parâmetros: a média (µ), que determina o centro da curva, e o desvio padrão (σ), que mede a dispersão ou o espalhamento dos dados em torno da média.
3. Aplicações em Saúde: Variáveis quantitativas contínuas como pressão arterial, níveis de colesterol, estatura e peso ao nascer em uma população frequentemente seguem uma distribuição de dados que pode ser bem aproximada pela curva normal.

Aplicação Prática: Análise de Níveis de Colesterol

Para avaliar o peso do colesterol alto e identificar segmentos de alto risco na população, um analista de saúde pública precisa entender a probabilidade de observar certos níveis de colesterol. A Distribuição Normal fornece o modelo para isso.

Cenário: Um pesquisador deseja saber a probabilidade de um indivíduo selecionado aleatoriamente ter uma taxa de colesterol menor que 195 mg/100ml. Estudos prévios indicam que, na população, a taxa média de colesterol (µ) é de 200 mg/100ml com um desvio padrão (σ) de 20 mg.

Para resolver isso, o pesquisador usa o modelo da Distribuição Normal. O primeiro passo é a padronização, que transforma o valor de interesse (X) em um escore-z, o qual mede quantos desvios padrão um valor está da média.

A fórmula é: z = (X - µ) / σ

Aplicando os valores do cenário: z = (195 - 200) / 20 = -5 / 20 = -0,25

Este escore-z significa que um nível de colesterol de 195 mg/100ml está 0,25 desvios padrão abaixo da média. Com esse valor, o pesquisador pode consultar uma tabela de distribuição normal padrão para encontrar a probabilidade acumulada correspondente, que é de aproximadamente 0,4013 ou 40,13%. Isso demonstra o imenso poder preditivo do modelo normal para estimar riscos e prevalências em nível populacional.

Mas o que acontece quando os dados não são contínuos e sim categóricos, como uma resposta “sim” ou “não” em uma pesquisa?

3. O Mundo Binário: Entendendo a Distribuição Binomial

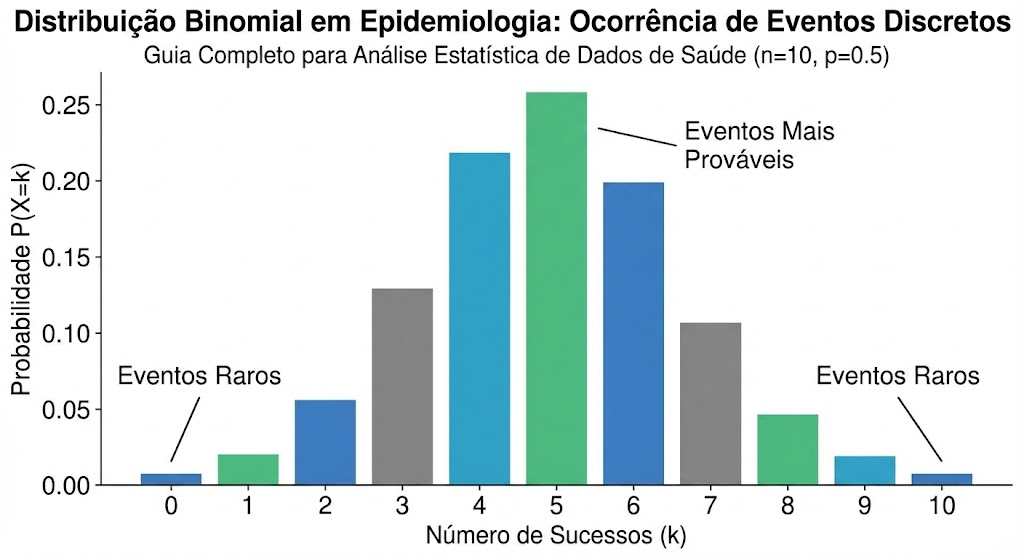
Em epidemiologia, muitos desfechos são dicotômicos: um indivíduo está doente ou não está, foi exposto a um fator de risco ou não foi, sobreviveu a um tratamento ou não. Para analisar a probabilidade desses eventos de natureza binária, a Distribuição Binomial oferece o modelo matemático perfeito. Ela nos permite calcular a probabilidade de obter um número específico de “sucessos” em um número fixo de tentativas.

Condições para a Distribuição Binomial

Para que um fenômeno possa ser modelado por uma Distribuição Binomial, ele precisa atender a quatro condições:

• Um número fixo de tentativas (n): O experimento é repetido um número pré-determinado de vezes (ex: entrevistar 500 pessoas).
• Cada tentativa é independente: O resultado de uma tentativa não influencia o de outra.
• Cada tentativa resulta em apenas dois resultados possíveis: Os resultados são classificados como “sucesso” ou “fracasso”.
• A probabilidade de sucesso (p) é constante: A probabilidade de um “sucesso” permanece a mesma em todas as tentativas.

Aplicação Prática em Saúde Coletiva

Exemplo: Proporção de Respostas em uma Pesquisa de Saúde

Imagine o seguinte cenário de saúde pública:

Um pesquisador quer estimar a proporção de pessoas em uma comunidade que receberam a vacina da gripe. Ele seleciona aleatoriamente e entrevista 500 pessoas, cujas respostas possíveis são “Sim” (sucesso) ou “Não” (fracasso).

Este cenário se encaixa perfeitamente no modelo binomial:

• n = 500 (o número fixo de entrevistados).
• A resposta de cada pessoa é independente.
• Há apenas dois resultados: “Sim” ou “Não”.
• p é a proporção (desconhecida) de pessoas vacinadas na população.

Com este modelo, o pesquisador pode calcular a probabilidade de observar um certo número de respostas “Sim” e estimar a média (µ = np) e a variância (σ² = np(1-p)) para essa distribuição de dados binomial, o que é fundamental para a realização de testes de hipóteses.

Agora, vamos mudar o foco de eventos binários para a contagem de eventos que são raros, mas que ocorrem ao longo do tempo ou em uma determinada área.

4. Contando Eventos Raros: A Distribuição de Poisson

Enquanto a Distribuição Binomial lida com o número de sucessos em um número fixo de tentativas, a Distribuição de Poisson é a ferramenta ideal para modelar o número de vezes que um evento ocorre em um intervalo fixo de tempo ou espaço, especialmente quando o evento é considerado raro. Na vigilância epidemiológica, sua aplicação é vasta e poderosa, ajudando a diferenciar flutuações aleatórias de sinais de alerta que merecem investigação.

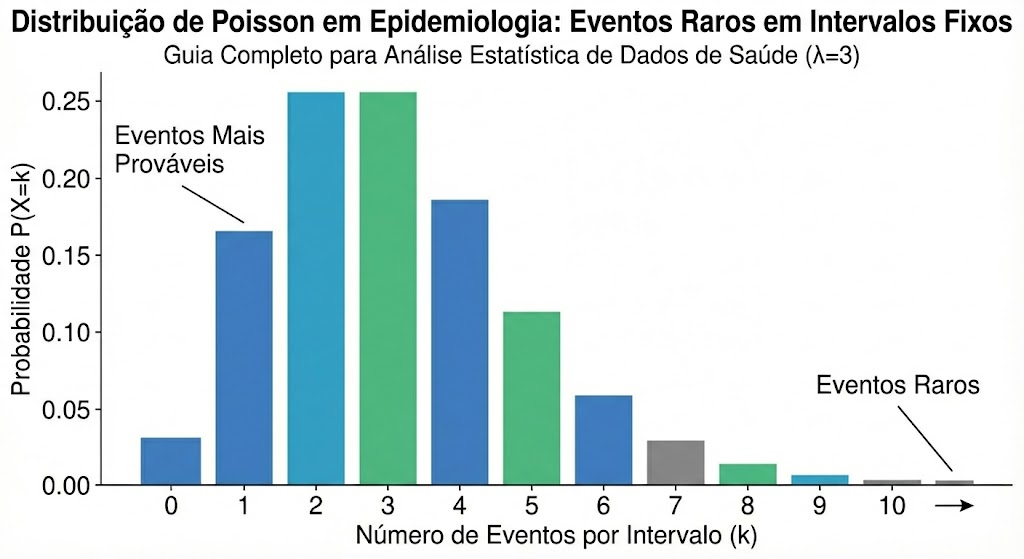
O Parâmetro Chave – Lambda (λ)

A Distribuição de Poisson é definida por um único parâmetro, λ (lambda), que representa a taxa média de ocorrência do evento naquele intervalo específico. Por exemplo, se em média um hospital registra 3 casos de uma doença rara por ano, então λ = 3. Esse valor define toda a distribuição e nos permite calcular a probabilidade de observar qualquer outro número de casos.

Aplicação Prática em Epidemiologia

No seu trabalho, você verá a Distribuição de Poisson aplicada para modelar taxas de doenças não comunicáveis raras, o número mensal de acidentes com agulhas em um hospital ou o número de mutações genéticas em uma sequência de DNA. Em cada caso, λ representa a taxa de base conhecida, e o modelo testa se um aglomerado observado é uma anomalia estatística que exige investigação.

Exemplo: Incidência de uma Doença Genética Rara

A aplicação mais poderosa da Poisson em epidemiologia é na construção de diagramas de controle para identificar surtos.

Suponha que a taxa histórica de hemofilia em nascidos do sexo masculino seja de 1 a cada 5.000. Em uma região com 2.000.000 de nascimentos masculinos em um período, a taxa esperada de casos, nosso λ, seria de 400. Este valor representa o nível endêmico ou a linha de base em um diagrama de controle.

A Distribuição de Poisson ajuda a definir os limites de variação esperada em torno dessa média. Se os oficiais de saúde pública observassem 450 casos no mesmo período, eles poderiam usar o modelo de Poisson para calcular a probabilidade de observar 450 ou mais casos, dado que a média esperada é 400. Se essa probabilidade for extremamente baixa (por exemplo, p < 0,01), o número observado excede o limite superior do diagrama de controle. Isso é precisamente o que dispara um alerta de epidemia, fornecendo evidência estatística de que o aumento não é fruto do acaso e justifica uma investigação aprofundada.

Conclusão: A Distribuição de Dados Como Bússola Analítica

A análise da distribuição de dados não é uma mera formalidade estatística, mas a bússola que guia o epidemiologista através do complexo terreno da análise de dados em saúde. Desde a escolha da ferramenta estatística correta até a validade final das inferências sobre a saúde de uma população, a compreensão da forma subjacente dos dados é o que separa uma análise robusta de uma conclusão frágil.

Ao finalizar este guia, lembre-se destes pontos-chave:

• A Distribuição Normal é o pilar para variáveis contínuas e a base para a maioria dos testes paramétricos.
• A Distribuição Binomial é essencial para modelar desfechos dicotômicos e analisar proporções em pesquisas e estudos.
• A Distribuição de Poisson é a ferramenta de escolha para a contagem de eventos raros e um pilar da vigilância epidemiológica.
• Este guia focou nos pilares fundamentais, mas a epidemiologia moderna também lida com dados que não se encaixam nesses modelos, como dados assimétricos de custos de saúde (muitas vezes modelados pela distribuição Gama) ou dados de contagem com mais variabilidade do que o esperado (superdispersão), que exigem modelos como o Binomial Negativo.

Identificar corretamente a distribuição dos seus dados é o que transforma sua análise de um exercício técnico em uma ferramenta essencial para proteger a saúde da população.

——————————————————————————–

FAQ: Perguntas e Respostas sobre Distribuição de Dados

1. O que é distribuição de dados em estatística? A distribuição de dados é uma função ou um gráfico que descreve todos os valores possíveis que uma variável pode assumir e com que frequência eles ocorrem. Em essência, ela mostra a “forma” dos seus dados, indicando se eles são simétricos, assimétricos, ou se concentram em torno de um valor central.
2. Por que a Distribuição Normal é tão importante em bioestatística? A Distribuição Normal é crucial porque muitos fenômenos biológicos (como altura, peso e pressão arterial) tendem a seguir este padrão. Além disso, muitos testes estatísticos poderosos, chamados de testes paramétricos, exigem que os dados sigam uma distribuição normal para que seus resultados sejam válidos.
3. Quando devo usar a Distribuição Binomial em um estudo epidemiológico? Use a Distribuição Binomial quando seu desfecho de interesse for dicotômico, ou seja, só pode ter dois resultados (ex: presença ou ausência de uma doença, sucesso ou fracasso de um tratamento). Ela é ideal para calcular a probabilidade de um certo número de “sucessos” em um número fixo de observações.
4. Qual a principal aplicação da Distribuição de Poisson em saúde pública? Sua principal aplicação é na vigilância epidemiológica para modelar a contagem de eventos raros em um intervalo de tempo ou espaço, como o número de novos casos de uma doença rara por mês. Ela é fundamental para criar diagramas de controle e identificar surtos.
5. Como um histograma me ajuda a entender a distribuição dos meus dados? Um histograma é uma representação gráfica que agrupa seus dados em intervalos e mostra a frequência em cada um. Ele permite visualizar rapidamente a forma da sua distribuição de dados, identificar o valor central, avaliar a dispersão e detectar a presença de assimetria ou valores atípicos.
6. O que fazer quando meus dados não seguem uma distribuição normal? Você pode tentar transformar os dados (ex: com uma transformação logarítmica) para aproximá-los de uma distribuição normal. A abordagem mais segura, no entanto, é utilizar testes estatísticos não paramétricos, que não fazem suposições sobre a distribuição. Exemplos incluem o teste de Mann-Whitney U em vez de um teste-t, ou o de Kruskal-Wallis em vez de uma ANOVA.
7. Qual a diferença entre a distribuição de dados na amostra e na população? A distribuição na amostra é o padrão que você observa nos dados que coletou. A distribuição na população é o padrão verdadeiro e completo de todos os indivíduos, que geralmente é desconhecido. O objetivo da estatística inferencial é usar a distribuição da amostra para fazer suposições e tirar conclusões sobre a distribuição da população.