1. Introdução: Por Que Olhar Através do Tempo?
Dados longitudinais são informações coletadas de um mesmo grupo de indivíduos ou de uma mesma população em múltiplos momentos ao longo do tempo. Na saúde pública, essa perspectiva temporal não é apenas útil, é fundamental. Enquanto um estudo transversal nos oferece um “retrato” da saúde em um único instante, a análise longitudinal nos entrega o “filme”, permitindo observar a progressão de doenças, o impacto de exposições ao longo da vida e as complexas relações de causa e efeito.
A limitação de análises pontuais é evidente quando consideramos os determinantes sociais da saúde, que exercem sua influência ao longo de toda a vida. Como bem resume a literatura especializada:
“Estudos com dados sobre circunstâncias socioeconômicas em apenas uma fase da vida são inadequados para elucidar completamente a contribuição dos fatores socioeconômicos para a saúde e o risco de mortalidade.”
Vamos abordar adiante uma visão estruturada sobre os desenhos de estudo, as técnicas de análise e a interpretação de dados longitudinais, para compreender melhor como investigamos a saúde de forma dinâmica. Para quantificar as mudanças na saúde ao longo do tempo, a epidemiologia se baseia em métricas fundamentais que diferenciam o “estoque da doença” do seu “fluxo”.
2. Fundamentos: As Métricas da Mudança em Saúde
Para estudar a ocorrência de doenças ao longo do tempo, a epidemiologia utiliza duas medidas essenciais: incidência e prevalência. Compreender a distinção entre elas é o primeiro passo para uma análise longitudinal correta.
| Característica | Incidência | Prevalência |
| O que mede | A ocorrência de casos novos de uma doença em uma população. | A proporção de casos existentes (novos + antigos) em uma população em um momento específico. |
| Tipo de informação | Fornece uma medida do risco de adoecer. Reflete a “velocidade” com que novos casos surgem. | Fornece uma medida da carga da doença na população. Reflete o fardo total da condição de saúde. |
| Numerador Típico | Número de casos novos em um período de tempo. | Número total de casos (novos e antigos) em um ponto no tempo. |
| Denominador Típico | População em risco de desenvolver a doença durante o mesmo período. | População total no mesmo ponto no tempo. |
A principal força dos estudos longitudinais é a capacidade de estabelecer a relação temporal entre uma exposição e um desfecho. Para inferir causalidade, é fundamental que a exposição (ex: um fator de risco) ocorra antes do desfecho (ex: o desenvolvimento da doença). Por exemplo, a análise longitudinal permite demonstrar que a exposição ao tabagismo durante a vida adulta precede o desenvolvimento de câncer de pulmão, fortalecendo a evidência de uma ligação causal.
Compreendidas as métricas essenciais, a questão que se segue é metodológica: como obtemos dados que nos permitam calcular a incidência e estabelecer a temporalidade? A resposta reside nos desenhos de estudo longitudinais, sendo o estudo de coorte o arquétipo para medir o risco diretamente.
3. Desenhos de Estudo para Coleta de Dados Longitudinais
A coleta de dados longitudinais é o pilar da epidemiologia analítica. Diferentes desenhos de estudo são empregados para seguir populações e investigar associações ao longo do tempo.
| Desenho do Estudo | Ponto de Partida | Principal Medida de Associação | Principal Vantagem |
| Estudo de Coorte (Prospectivo e Retrospectivo) | Seleciona grupos de indivíduos expostos e não expostos a um fator de risco e os acompanha ao longo do tempo. | Risco Relativo (RR) e Hazard Ratio (HR) | Permite o cálculo direto da incidência e estabelece claramente a sequência temporal entre exposição e desfecho. |
| Estudo de Caso-Controle | Seleciona indivíduos que já têm a doença (casos) e um grupo comparável que não tem a doença (controles). | Odds Ratio (OR) | Eficiente para estudar doenças raras e desfechos com longo período de latência, pois reconstrói a história de exposição passada. |
| Ensaio Clínico Randomizado (ECR) | Aloca aleatoriamente participantes para um grupo de intervenção (ex: novo tratamento) ou um grupo de controle (ex: placebo ou tratamento padrão). | Risco Relativo (RR), Eficácia | Considerado o “padrão ouro” para avaliar a eficácia de intervenções, pois a randomização minimiza vieses de seleção e confundimento. |
- Estudo de Coorte: É o desenho longitudinal por excelência, projetado especificamente para medir a incidência diretamente ao acompanhar uma população em risco ao longo do tempo. Grupos são classificados com base em sua exposição e seguidos para comparar a ocorrência de desfechos. O Whitehall Study, por exemplo, foi um estudo de coorte que acompanhou funcionários públicos britânicos por 10 anos para investigar como a categoria profissional (exposição) se relacionava com a mortalidade (desfecho).
- Estudo de Caso-Controle: Embora parta do desfecho, este estudo tem uma natureza longitudinal implícita ao investigar exposições ocorridas no passado. O desafio metodológico, e a chave para sua validade, é selecionar controles que representem a mesma “coorte imaginária” da qual os casos se originaram. Ao fazer isso, estamos efetivamente amostrando o denominador (o tempo-pessoa em risco) daquela coorte. Isso permite que o Odds Ratio (OR), a medida de associação calculada neste desenho, seja uma estimativa válida do Risco Relativo que teria sido medido em um estudo de coorte completo. Como nota um professor experiente, sob a condição de que a doença seja rara na população, o OR é uma excelente aproximação do Risco Relativo. Essa eficiência para doenças raras deriva do fato de que um estudo de coorte para uma doença rara exigiria uma amostra imensa seguida por um longo período para acumular casos suficientes — um processo proibitivamente caro e demorado. O desenho de caso-controle contorna esse problema ao partir dos casos já existentes.
- Ensaio Clínico Randomizado: É um tipo de estudo de coorte experimental. Ao seguir os grupos de intervenção e controle ao longo do tempo, ele avalia se a intervenção causa uma mudança no desfecho. Variações como o desenho cross over, onde os participantes trocam de grupo após um período, adicionam uma camada extra de comparação longitudinal dentro dos mesmos indivíduos.
A coleta de dados ao longo do tempo através de desenhos robustos é apenas o primeiro passo. O desafio seguinte é destilar essa complexa informação, distribuída em múltiplas camadas temporais, em padrões compreensíveis, o que se inicia com a análise descritiva.
4. Técnicas de Análise Descritiva e Básica
O primeiro passo em qualquer análise de dados longitudinais é explorar e resumir as informações coletadas para identificar tendências e padrões.
Análise Gráfica
- Gráficos de Linhas: São a ferramenta mais intuitiva para visualizar como uma variável muda ao longo do tempo. Cada ponto no gráfico representa o valor da variável em um momento específico, e as linhas que os conectam revelam a trajetória da mudança.
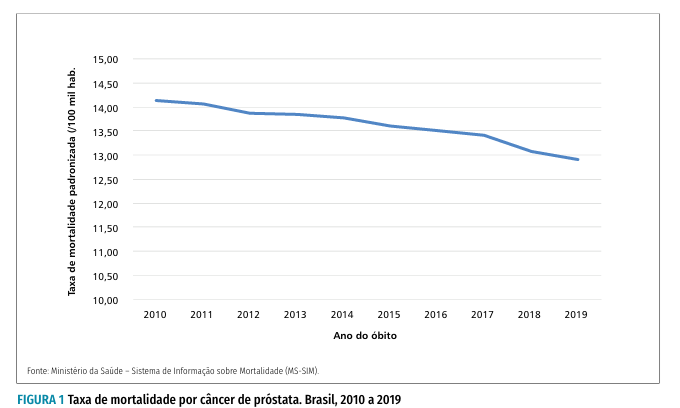
Análise de Sobrevida
Este conjunto de técnicas é central para a análise de dados do tipo “tempo até o evento”, onde o desfecho de interesse é a ocorrência de um evento (ex: óbito, diagnóstico, cura) e o tempo que levou para ele ocorrer.
- Tabelas de Vida (Método Atuarial): Este método clássico agrupa os dados de seguimento em intervalos de tempo fixos (ex: anos) e calcula a probabilidade de um indivíduo “sobreviver” (ou seja, não ter o evento) em cada intervalo. É útil quando os tempos exatos dos eventos não são conhecidos.
- Curvas de Kaplan-Meier: Uma abordagem mais precisa que utiliza os tempos exatos em que cada evento ocorre. O resultado é um gráfico em degraus (step function) que mostra a probabilidade de sobrevida diminuindo a cada ocorrência de um evento. É a técnica visual mais comum para apresentar os resultados de ensaios clínicos e estudos de coorte.

A análise descritiva revela tendências, mas para testar hipóteses e isolar o efeito de uma exposição específica em meio a múltiplos fatores de risco (confundidores), necessitamos de modelos estatísticos mais sofisticados.
5. Técnicas de Análise Avançada: Modelando o Risco ao Longo do Tempo
Para avaliar o impacto de um fator de risco enquanto se controla simultaneamente a influência de outras variáveis (confundidores), utilizamos modelos de regressão multivariáveis.
Regressão de Riscos Proporcionais de Cox
Este é, de longe, o modelo estatístico mais utilizado na análise de sobrevida em saúde pública. É um modelo semiparamétrico. Essa característica é sua grande vantagem, pois nos libera da necessidade de fazer suposições sobre a forma da função de sobrevida ao longo do tempo (a chamada linha de base do risco), tornando o modelo extremamente robusto e flexível para diversas aplicações.
- Objetivo Principal: Estimar como uma ou mais variáveis (ex: exposição a um fator de risco, grupo de tratamento) influenciam a taxa de ocorrência de um evento ao longo do tempo.
- Medida de Efeito: A principal medida de efeito gerada pelo modelo de Cox é o Hazard Ratio (HR).
- Interpretação do HR: O HR representa o risco instantâneo de ocorrência do evento no grupo exposto em comparação com o grupo não exposto, em qualquer ponto do tempo, após ajustar pelos outros fatores incluídos no modelo.
- HR = 1: Não há diferença no risco entre os grupos.
- HR > 1: O grupo exposto tem um risco maior de apresentar o evento.
- HR < 1: O grupo exposto tem um risco menor de apresentar o evento (efeito protetor).
- Interpretação do HR: O HR representa o risco instantâneo de ocorrência do evento no grupo exposto em comparação com o grupo não exposto, em qualquer ponto do tempo, após ajustar pelos outros fatores incluídos no modelo.
Breve Menção a Outros Modelos
Para análises ainda mais complexas de dados longitudinais, existem outras abordagens, que são tópicos para estudo aprofundado:
- Processos de Markov: Utilizados para modelar as transições dos indivíduos entre diferentes estados de saúde ao longo do tempo (ex: saudável → doente → curado → óbito).
- Análise de Séries Temporais: Aplicada a dados coletados em intervalos de tempo regulares (ex: taxas de mortalidade mensais) para identificar tendências, ciclos e sazonalidade.
Para solidificar a compreensão desses conceitos, desde o desenho do estudo até a modelagem multivariável, nada é mais eficaz do que aplicá-los a um exemplo prático.
6. Aplicação Prática: Um Estudo de Caso sobre Desigualdades em Saúde
Estudo de Caso: Fatores Socioeconômicos ao Longo da Vida e Mortalidade por Doença Cardiovascular (DCV)
Vamos simular o fluxo de uma análise longitudinal para investigar a relação entre posição social e saúde, inspirado em estudos clássicos como o Whitehall Study.
Passo 1: A Pergunta de Pesquisa
Como a posição socioeconômica, medida pela categoria profissional, impacta o risco de mortalidade por DCV ao longo do tempo, mesmo após controlar por fatores de risco conhecidos como o tabagismo?
Passo 2: O Desenho do Estudo
Utilizaríamos um estudo de coorte prospectivo. Uma população de funcionários públicos seria recrutada e classificada de acordo com sua categoria profissional no início do estudo em: administrativas, profissionais/executivas, de escritório (clerical) e “outras” (principalmente mensageiros e trabalhadores manuais). Todos os participantes seriam acompanhados por mais de uma década, e os óbitos por DCV seriam registrados durante o período de seguimento. Fatores como idade e tabagismo também seriam medidos no início.
Passo 3: A Análise
- Análise Descritiva:
- O primeiro passo revelaria um claro gradiente social na mortalidade. As taxas de mortalidade por DCV, ajustadas por idade, seriam progressivamente maiores à medida que se desce na hierarquia profissional, das categorias administrativas para as “outras” (trabalhadores manuais).
- Análise de Sobrevida:
- A construção de Curvas de Kaplan-Meier para cada categoria profissional (administrativas, profissionais/executivas, etc.) mostraria visualmente que a probabilidade de sobrevida sem um evento fatal de DCV é consistentemente menor para os grupos de menor categoria profissional ao longo do tempo de acompanhamento.
- Análise Multivariável:
- Para isolar o efeito da categoria profissional, um modelo de Regressão de Cox seria aplicado. A saída do modelo forneceria um Hazard Ratio (HR) para cada categoria profissional em comparação com a categoria de referência (administrativa), com ajuste estatístico para os efeitos da idade e do tabagismo.
Passo 4: A Interpretação
Se o modelo de Cox produzisse um HR significativamente maior que 1 para as categorias profissionais mais baixas, mesmo após o ajuste, teríamos forte evidência de que a posição socioeconômica é um fator de risco independente para a mortalidade por DCV. Este resultado apoiaria a conclusão de que “fatores socioeconômicos que atuam ao longo da vida afetam a saúde e o risco de morte prematura.”
Este exemplo ilustra o poder único da análise longitudinal para desvendar as complexas teias de causalidade que determinam a saúde das populações.
7. Conclusão: O Poder da Perspectiva Longitudinal
A análise de dados longitudinais é uma ferramenta indispensável na saúde pública moderna. Sua força reside em sua capacidade de ir além das associações estáticas e investigar os processos dinâmicos de saúde e doença.
Recapitulando os pontos principais:
- A análise longitudinal é indispensável para entender a causalidade, a progressão da doença e o impacto de exposições ao longo do ciclo de vida.
- Desenhos de estudo como coortes e ensaios clínicos são as ferramentas primárias para coletar dados longitudinais robustos.
- Técnicas como a análise de sobrevida e a Regressão de Cox permitem não apenas descrever, mas também modelar o risco ao longo do tempo, controlando por múltiplos fatores.
Enquanto a análise transversal oferece uma fotografia, a análise longitudinal nos entrega o filme. É essa perspectiva dinâmica que permite uma compreensão profunda dos determinantes da saúde, sendo essencial para a formulação de políticas públicas equitativas.
8. Referências
- Blane D, Hart CL, Davey Smith G, Gillis CR, Hole DJ, Hawthorne VM. Association of cardiovascular disease risk factors with socioeconomic position during childhood and during adulthood. BMJ. 1996;313:1434-8.
- Davey Smith G. Reflections on the limitations of epidemiology. J Clin Epidemiol. 2001;54:325-31.
- Diez-Roux AV. Bringing context back into epidemiology: variables and fallacies in multilevel analysis. Am J Public Health. 1998;88:216-22.










