Medidas de Tendência Central: Média, Mediana e Moda. Domine a Interpretação dos Dados.

1. Introdução: O Primeiro Passo na Análise de Dados de Saúde

Em saúde pública e na epidemiologia, somos constantemente confrontados com vastos volumes de dados brutos — prontuários de pacientes, resultados de exames laboratoriais, registros de óbitos e dados de inquéritos populacionais [1]. Para que esses dados se transformem em conhecimento acionável, o primeiro e mais importante passo é a sua sumarização. As Medidas de Tendência Central (MTC) são as ferramentas fundamentais para essa tarefa, permitindo-nos destilar a complexidade de milhares de observações em um único valor que represente o “centro” ou o “valor típico” do conjunto. A capacidade de resumir dados de forma precisa é de importância estratégica, pois subsidia desde a decisão clínica individual até o planejamento de políticas públicas de larga escala.

Neste relatório, exploraremos as três principais MTC: a Média Aritmética, a Mediana e a Moda. Embora seus cálculos sejam relativamente simples, a escolha correta entre elas representa uma das decisões mais críticas na análise de dados de saúde. Uma seleção inadequada pode levar a conclusões enviesadas, mascarando realidades importantes sobre a saúde de uma população e resultando em intervenções desnecessárias ou ineficazes [2]. Compreender as nuances de cada medida é, portanto, uma habilidade essencial para qualquer profissional da área.

Vamos agora mergulhar em um estudo detalhado de cada uma dessas três medidas, começando pela mais conhecida e frequentemente utilizada: a Média Aritmética.

2. A Trindade da Centralidade: Definição e Cálculo

Dominar a definição e o cálculo de cada medida de tendência central é a base para uma análise de dados robusta. A Média, a Mediana e a Moda podem ser entendidas como três “lentes” distintas para observar o centro de um conjunto de dados. Cada uma oferece uma perspectiva única, com forças e fraquezas que as tornam mais ou menos adequadas dependendo da natureza e da distribuição dos dados em análise.

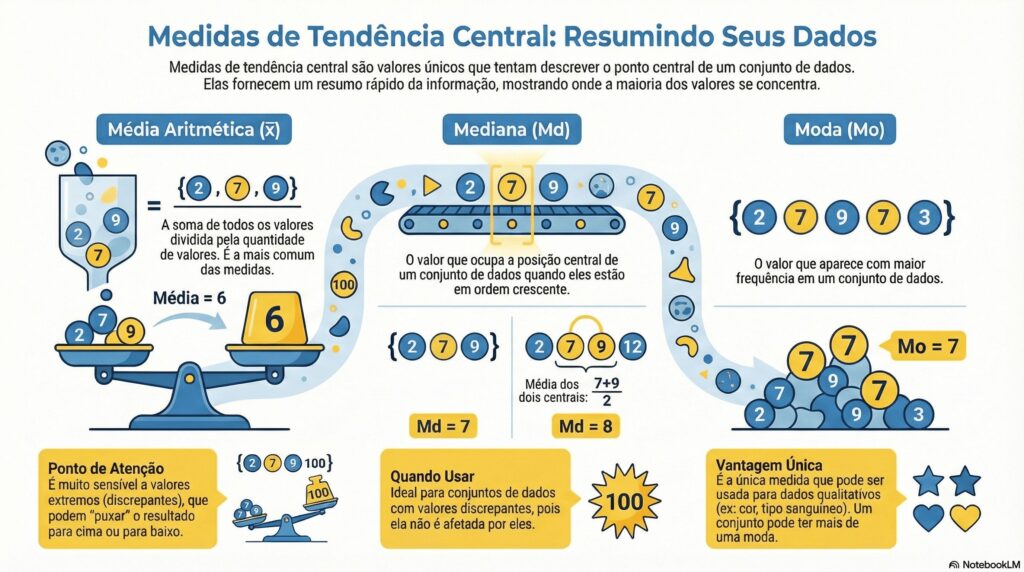
2.1. A Média Aritmética: O “Ponto de Equilíbrio”

A Média Aritmética, comumente chamada apenas de “média”, é a medida mais popular de tendência central. Ela é calculada somando-se todos os valores de um conjunto de dados e dividindo-se o resultado pelo número total de observações. Uma analogia útil é pensar na média como o “centro de gravidade” dos dados; se os valores fossem pesos distribuídos em uma régua, a média seria o ponto de equilíbrio. Sua principal característica — e também sua maior vulnerabilidade — é sua sensibilidade a todos os valores do conjunto, o que significa que valores extremamente altos ou baixos (conhecidos como outliers) podem distorcê-la significativamente [2].

2.2. A Mediana: O “Valor Posicional”

A Mediana é o valor que ocupa a posição central de um conjunto de dados quando estes estão organizados em ordem crescente ou decrescente [3]. Ela divide o conjunto de dados em duas metades iguais: 50% dos valores estão abaixo da mediana e 50% estão acima. Se o conjunto de dados tiver um número ímpar de observações, a mediana é o valor do meio. Se tiver um número par, a mediana é a média dos dois valores centrais.

A principal virtude da Mediana é sua robustez. Ao contrário da Média, a Mediana não é afetada por valores extremos. Essa característica a torna uma representação muito mais fiel do “valor típico” em conjuntos de dados que apresentam observações discrepantes ou distribuição assimétrica, um cenário extremamente comum em dados biológicos e socioeconômicos, como renda ou tempo de sobrevida [2, 4]. A média, ao ser “puxada” por esses valores extremos, pode oferecer uma visão distorcida da realidade da maioria dos indivíduos da amostra [2].

2.3. A Moda: O “Valor Mais Frequente”

A Moda é simplesmente o valor que aparece com maior frequência em um conjunto de dados. Um conjunto de dados pode não ter moda (se todos os valores aparecem com a mesma frequência), ter uma moda (unimodal), duas modas (bimodal) ou mais (multimodal). Sua principal utilidade reside na análise de dados categóricos nominais (como tipo sanguíneo ou etnia), onde o cálculo da média ou da mediana não faz sentido. Em dados numéricos, a moda é menos utilizada, mas pode ser útil para identificar picos de frequência em uma distribuição.

2.4. Exemplo de Cálculo

Vamos considerar um cenário com dados de pressão arterial sistólica (em mmHg) de uma amostra de 9 pacientes, inspirado em dados de saúde [1]: Dados: {140, 100, 140, 165, 170, 150, 155, 160, 175}

1. Cálculo da Média:
   • Passo 1: Somar todos os valores.
     • 140 + 100 + 140 + 165 + 170 + 150 + 155 + 160 + 175 = 1355
   • Passo 2: Dividir a soma pelo número de observações (n=9).
     • 1355 / 9 = 150,56
   • Resultado: A Média da pressão sistólica é 150,56 mmHg.
2. Cálculo da Mediana:
   • Passo 1: Ordenar os dados em ordem crescente.
     • {100, 140, 140, 150, 155, 160, 165, 170, 175}
   • Passo 2: Identificar o valor na posição central. Como temos 9 observações (um número ímpar), a posição central é a 5ª.
   • Resultado: A Mediana da pressão sistólica é 155 mmHg.
3. Cálculo da Moda:
   • Passo 1: Identificar o valor que mais se repete no conjunto de dados.
   • Resultado: O valor 140 mmHg aparece duas vezes, mais do que qualquer outro valor. Portanto, a Moda é 140 mmHg.

Embora o cálculo seja direto, a verdadeira maestria reside em saber qual dessas medidas utilizar em cada situação, uma decisão que depende inteiramente do formato da distribuição dos dados.

O Impacto da Distribuição: Simetria e Assimetria

Os dados coletados em estudos de saúde raramente são perfeitamente organizados. A “forma” ou “distribuição” desses dados é o fator mais importante na escolha da medida de tendência central mais apropriada. Compreender essa forma nos permite selecionar a medida que melhor representa a realidade, evitando interpretações enganosas. Os dois cenários principais que encontramos são a simetria e a assimetria.

3.1. O que é uma Distribuição de Dados?

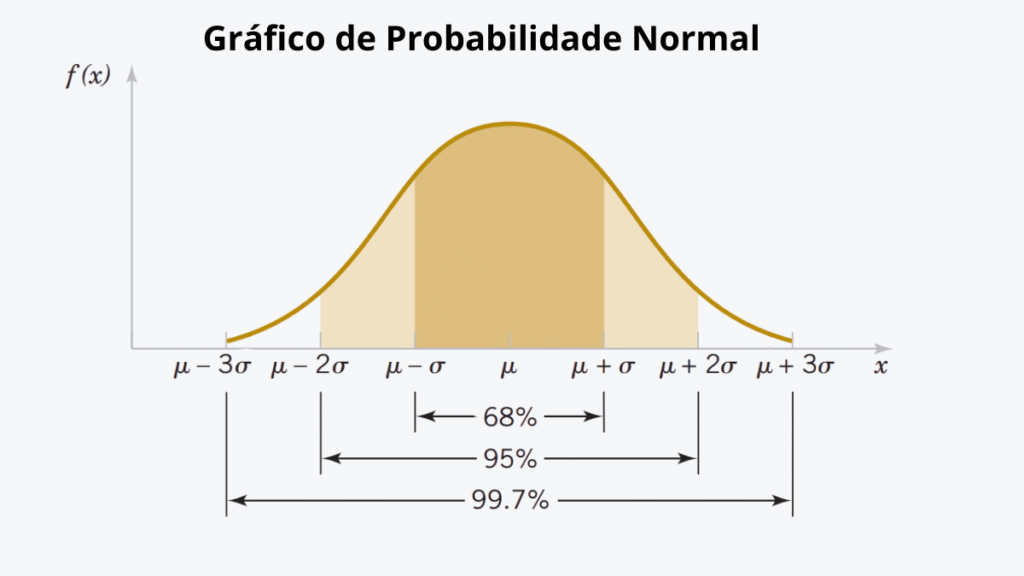
Uma distribuição de dados é uma representação gráfica ou matemática que mostra a frequência com que diferentes valores ocorrem em um conjunto de dados. O exemplo mais clássico de uma distribuição simétrica é a Distribuição Normal (ou Curva de Gauss), que tem um formato de sino. Nesta distribuição, a maioria dos valores se aglomera em torno do centro (a média), e a frequência diminui de forma igual para ambos os lados, criando uma imagem espelhada.

3.2. O Cenário Ideal: Distribuição Simétrica

Em uma distribuição perfeitamente simétrica, como a Normal, as três medidas de tendência central coincidem em um único ponto [2].

Média = Mediana = Moda

Neste cenário, a Média Aritmética é frequentemente a medida de escolha. Por considerar todos os valores do conjunto de dados, ela utiliza toda a informação disponível, tornando-se um resumo muito eficiente do centro dos dados.

3.3. Cenários Reais: A Assimetria

Na prática, muitas variáveis biológicas, sociais e econômicas não seguem uma distribuição perfeitamente simétrica. A presença de valores extremos em uma das “caudas” da distribuição cria o que chamamos de assimetria.

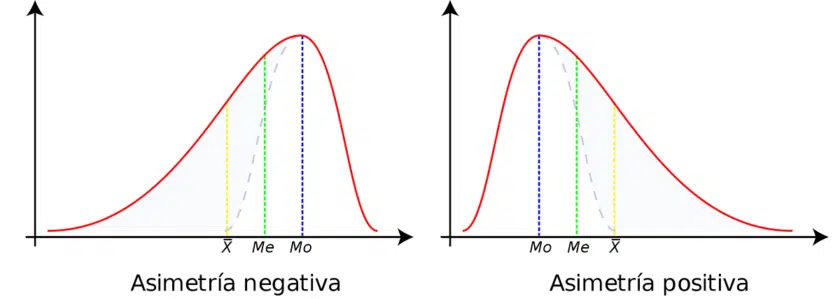
3.3.1. Assimetria à Direita (Positiva)

Esta é a forma mais comum em dados de saúde e socioeconômicos. Ocorre quando há uma concentração de valores mais baixos e uma cauda longa de valores altos à direita. Exemplos clássicos incluem renda, número de consultas médicas por ano ou o tempo de permanência hospitalar. Nesses casos, os poucos valores muito altos (outliers) “puxam” a Média para a direita, inflando seu valor [2]. A relação entre as medidas se torna:

Média > Mediana

Neste cenário, a Mediana se torna a medida mais representativa, pois indica o verdadeiro ponto central que divide a população, não sendo afetada pelos valores extremos que distorcem a média.

3.3.2. Assimetria à Esquerda (Negativa)

Este cenário é menos comum, mas também ocorre. Acontece quando a cauda da distribuição se estende para a esquerda, devido a valores anormalmente baixos. Um exemplo poderia ser a idade de óbito por uma doença que raramente afeta jovens, mas que tem alguns casos precoces. Aqui, a Média é “puxada” para a esquerda pelos valores baixos. A relação se inverte:

Média < Mediana

A compreensão da assimetria nos leva diretamente à regra de ouro para escolher a medida mais honesta e representativa para nossos dados.

4. A Combinação Vencedora: Escolhendo a Medida Certa

A escolha da medida de tendência central não é apenas uma formalidade estatística; é uma decisão estratégica e ética. O objetivo é sempre selecionar a medida que melhor representa a realidade da maioria da amostra, resistindo à influência enganosa de valores atípicos que podem levar a conclusões e, consequentemente, a ações equivocadas.

4.1. A Regra de Ouro da Robustez

Podemos sintetizar a decisão com uma regra simples e poderosa:

• Para distribuições assimétricas ou na presença de outliers significativos, prefira a Mediana. Ela é uma medida “robusta”, pois não é influenciada por valores extremos.
• Para distribuições simétricas e sem outliers importantes, a Média é uma excelente escolha, pois utiliza toda a informação contida nos dados.
• Para dados categóricos nominais, a Moda é a medida de escolha.

4.2. Guia Prático para Dados em Saúde

Vejamos alguns exemplos práticos com variáveis comuns em estudos epidemiológicos e de saúde pública [1, 4]:

• Quando usar a Média:
  • Idade em um grupo etário específico e bem definido (ex: escolares de 10 a 12 anos), onde a distribuição tende a ser simétrica.
  • Índice de Massa Corporal (IMC) em uma população geral, que frequentemente se aproxima de uma distribuição normal.
  • Medidas fisiológicas controladas, como a temperatura corporal em indivíduos saudáveis.
• Quando usar a Mediana:
  • Renda Familiar: Uma variável classicamente assimétrica à direita, onde a maioria das famílias tem renda baixa ou média, mas uma pequena minoria tem rendas extremamente altas [4]. A média da renda seria artificialmente inflada por essa minoria.
  • Tempo de Sobrevida após um Diagnóstico: Muitas pessoas podem ter uma sobrevida curta, enquanto algumas poucas vivem por muitos anos, criando uma cauda longa à direita.
  • Concentração de um Marcador Biológico Raro: Em um exame de sangue, a maioria dos indivíduos pode ter níveis indetectáveis ou muito baixos de um marcador, com alguns poucos apresentando concentrações altíssimas devido a uma condição específica.

4.3. Tabela Resumo: “Guia de Escolha: Média, Mediana ou Moda?”

Medida	Quando Usar (Tipo de Dado e Distribuição)	Principal Vantagem
Média	Dados numéricos com distribuição simétrica, sem outliers significativos.	Utiliza toda a informação do conjunto de dados, sendo estatisticamente poderosa.
Mediana	Dados numéricos com distribuição assimétrica ou com a presença de outliers.	Robusta à influência de valores extremos, representando melhor o “valor típico” da maioria.
Moda	Dados categóricos (nominais). Útil para identificar picos em distribuições numéricas.	Simples de identificar e a única medida aplicável a dados puramente qualitativos.

A aplicação correta desses conceitos é fundamental para a interpretação de estudos e para a comunicação de resultados, como veremos no estudo de caso a seguir.

5. Exemplo Aplicado em Epidemiologia: Análise de Renda e Saúde

A análise de fatores socioeconômicos é um pilar da epidemiologia, pois as desigualdades sociais se manifestam diretamente no corpo e nos desfechos de saúde de uma população [5]. Vamos explorar um cenário de estudo epidemiológico fictício, mas realista, para ilustrar o impacto da escolha da medida de tendência central.

• Cenário do Estudo: Um grupo de epidemiologistas está analisando a renda familiar mensal de uma comunidade de 10 famílias para avaliar a vulnerabilidade socioeconômica e planejar a alocação de recursos para um novo posto de saúde.
• Os Dados: A equipe coletou os seguintes dados de renda mensal. Os valores foram inspirados na realidade de desigualdade de renda, onde uma pequena parcela da população concentra uma grande fatia da renda total [4]. Renda Mensal (R$): {1.800, 2.100, 2.500, 2.800, 3.200, 3.500, 4.000, 7.000, 9.000, 45.000}
• A Análise Distorcida (usando a Média): Um analista apressado poderia calcular a média para descrever a renda “típica” da comunidade.
  • Cálculo da Média: (1.800 + 2.100 + 2.500 + 2.800 + 3.200 + 3.500 + 4.000 + 7.000 + 9.000 + 45.000) / 10 = R$ 8.090
  • Interpretação Equivocada: Se o relatório indicar que a renda média da comunidade é de **R 8.090**, os gestores de saúde poderiam concluir que a comunidade possui uma boa condição financeira. Essa interpretação, influenciada pelo único valor extremo de R 45.000, mascara a realidade de que 8 das 10 famílias (80% da amostra) ganham menos da metade desse valor. Isso poderia levar a políticas públicas equivocadas, como a subestimação da necessidade de programas de assistência social ou de subsídios.
• A Análise Correta (usando a Mediana): Um estatístico sênior, ciente da assimetria dos dados de renda, escolheria a mediana.
  • Cálculo da Mediana:
    1. Ordenar os dados: {1.800, 2.100, 2.500, 2.800, **3.200, 3.500**, 4.000, 7.000, 9.000, 45.000}
    2. Encontrar o valor central (média dos dois valores do meio, pois n=10): (3.200 + 3.500) / 2 = R$ 3.350
  • Interpretação Precisa: A renda mediana de R$ 3.350 representa com muito mais precisão a realidade socioeconômica da maioria das famílias. Este valor mostra que metade da comunidade vive com R 3.350 ou menos por mês, revelando uma vulnerabilidade que a média ocultou completamente.
• A Conclusão Epidemiológica: O “So What?” (E daí?) desta análise é profundo. A escolha da Mediana, neste caso, não é apenas uma preferência técnica, mas uma obrigação para revelar a verdadeira extensão da vulnerabilidade econômica. Com base na mediana, os gestores de saúde podem justificar a necessidade de programas de saúde direcionados, como subsídios para medicamentos, campanhas de nutrição e maior acesso a serviços gratuitos, que seriam considerados desnecessários se a análise se baseasse na média distorcida.

Este exemplo prático reforça que a escolha da medida de tendência central não é apenas uma questão de cálculo, mas uma responsabilidade fundamental na comunicação científica e na prática da saúde pública.

6. Conclusão: A Ética na Escolha da Medida Certa

Ao longo deste relatório, demonstramos que a Média, a Mediana e a Moda são mais do que simples ferramentas descritivas; são instrumentos de precisão que, quando bem utilizados, revelam a verdade contida nos dados. A escolha entre elas, especialmente entre a Média e a Mediana em contextos de dados de saúde e socioeconômicos com distribuições assimétricas, é uma decisão fundamental que impacta diretamente a interpretação dos resultados e as ações subsequentes. Apresentar os dados da forma mais honesta e representativa possível não é apenas uma boa prática estatística, mas um pilar da ética na comunicação científica e na prática epidemiológica. Um profissional de saúde consciente deve, portanto, dominar não apenas o cálculo, mas, sobretudo, o critério para selecionar a medida que melhor reflete a realidade da população que busca servir.

7. Referências

1. Sonia Vieira. Introdução à Bioestatística. 4ª ed. Rio de Janeiro: Elsevier; 2011.
2. Woodward M. Epidemiology: Study Design and Data Analysis. 3rd ed. Boca Raton: CRC Press; 2014.
3. Meneghel SN, et al. Epidemiologia: exercícios indisciplinados. Porto Alegre: Tomo Editorial; 2014.
4. Centro de Estudos Estratégicos da Fiocruz. Saúde e Desenvolvimento: o Complexo Econômico-Industrial da Saúde 4.0. Rio de Janeiro: CEE/Fiocruz; 2022.
5. Davey Smith G, Ben-Shlomo Y, Lynch J. Health inequalities: lifecourse approaches. Bristol: The Policy Press; 2010.

8. FAQ – Medidas de Tendência Central em Epidemiologia

8.1. O que são medidas de tendência central?

São estatísticas que resumem um conjunto de dados em um valor representativo, como média, mediana e moda.

8.2. Qual a diferença entre média, mediana e moda?

• Média: soma dos valores dividida pelo número de observações.
• Mediana: valor central quando os dados estão ordenados.
• Moda: valor que mais se repete no conjunto.

8.3. Quando usar a média?

Quando os dados são simétricos e não possuem valores extremos (outliers).

8.4. Quando usar a mediana?

Quando os dados são assimétricos ou possuem outliers, pois ela não é influenciada por valores extremos.

8.5. A moda é útil em epidemiologia?

Sim, especialmente para identificar categorias mais frequentes, como sintomas ou faixas etárias.

8.6. Como escolher a melhor medida?

Depende da distribuição dos dados:

• Distribuição normal → média
• Distribuição assimétrica → mediana
• Dados categóricos → moda

8.7. Qual a relação dessas medidas com a análise de saúde pública?

Elas ajudam a resumir informações populacionais, identificar padrões e apoiar decisões baseadas em evidências.